Optimisation heuristics in randomness testing

Karel Kubíček karel.kubicek@mail.muni.cz, master thesis, spring 2017

Keywords: randomness testing, cryptanalysis, block functions, stream functions, hash functions, problem optimization, metaheuristics

Abstract:

A detectable non-randomness of cryptoprimitive's output signals a bias of the cryptographic function. This bias may signal deeper security issues of the primitive. Therefore, statistical testing of randomness is one of the automated ways of cryptanalysis. Randomness assessment by statistical batteries is an example of such automated cryptanalysis. Research tool EACirc developed at Faculty of Informatics, Masaryk University aims to design the randomness tests, which adapts to the tested data. The tool utilises a simple heuristic based on local search. This thesis researches other metaheuristics and their influence on EACirc's success rate. In extension, proof of concept artificial neural network for randomness testing was analysed.

This thesis has three main contributions. The first is a development of a testbed of 16 well-known cryptographic functions used for randomness testing comparison. The second is an extension of EACirc by three new metaheuristics. One of them, called guided local search, outperforms all the others in terms of its success rate. The third contribution is an analysis of randomness tests produced by EACirc computation. Successful tests contain evidence of the bias in the tested data. The influence of tested metaheuristics on the complexity of these tests is analysed. It is shown that the guided local search produces the least complex tests, such that allow easier cryptanalysis.

Download thesis pdf, presentation pdf
Download dataset
List of tools:

@thesis{kubicekMasterThesis,
    author = {Karel Kubíček},
    supervisor = {Petr Švenda}, 
    title = {{Optimisation heuristics in randomness testing}},
    type = {Master thesis},
    institution = {Faculty of Informatics Masaryk University},
    year = {2017},
    url = {http://is.muni.cz/th/408351/fi_m/},
}

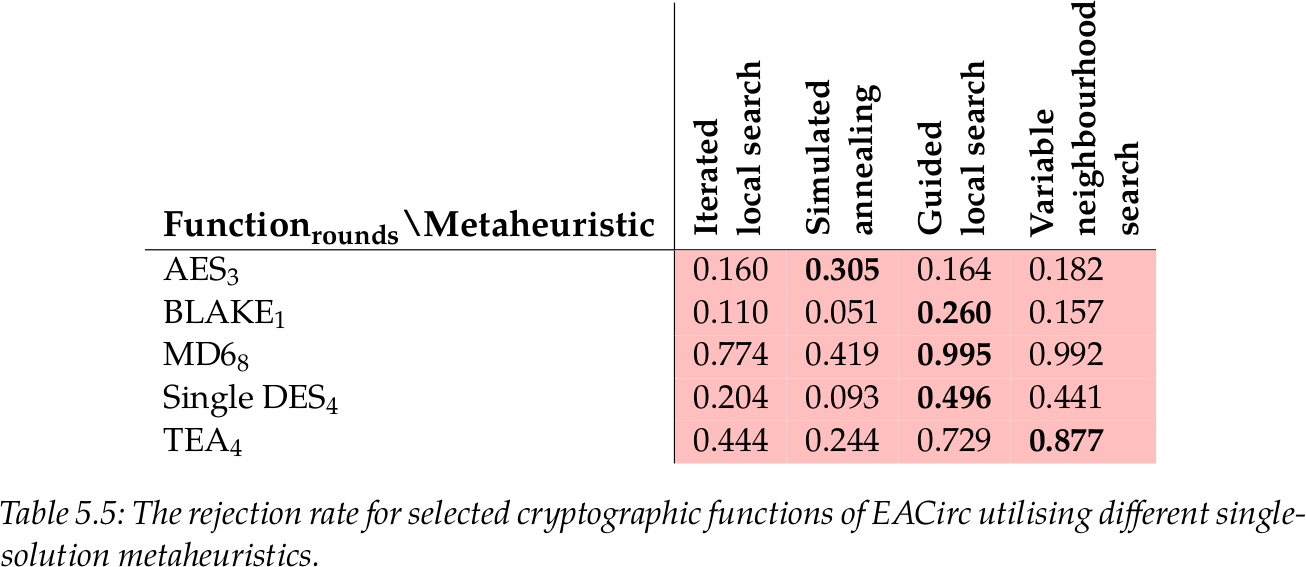
We analysed application of three single-solution metaheuristics in randomness testing tool EACirc. They all performed similarly, over the testbed of 16 functions, only five of them showed some differences. The differences are showed in following figure. The numbers are rejection rate of EACirc - how often the metaheuristic produces a randomness test capable of distinguishing selected data.

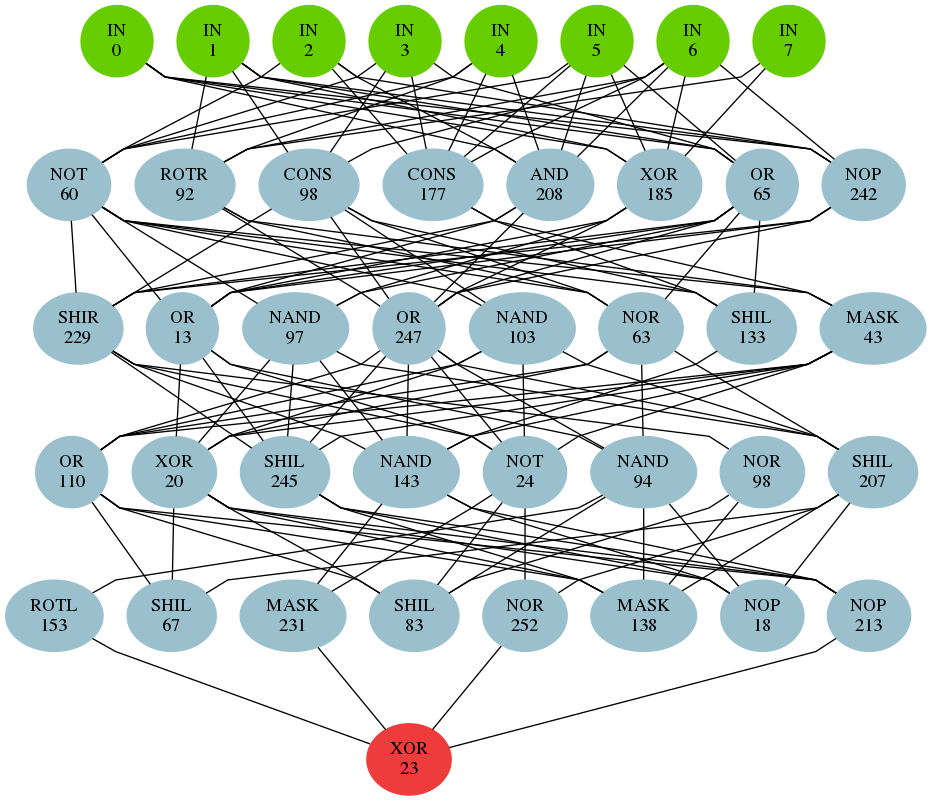
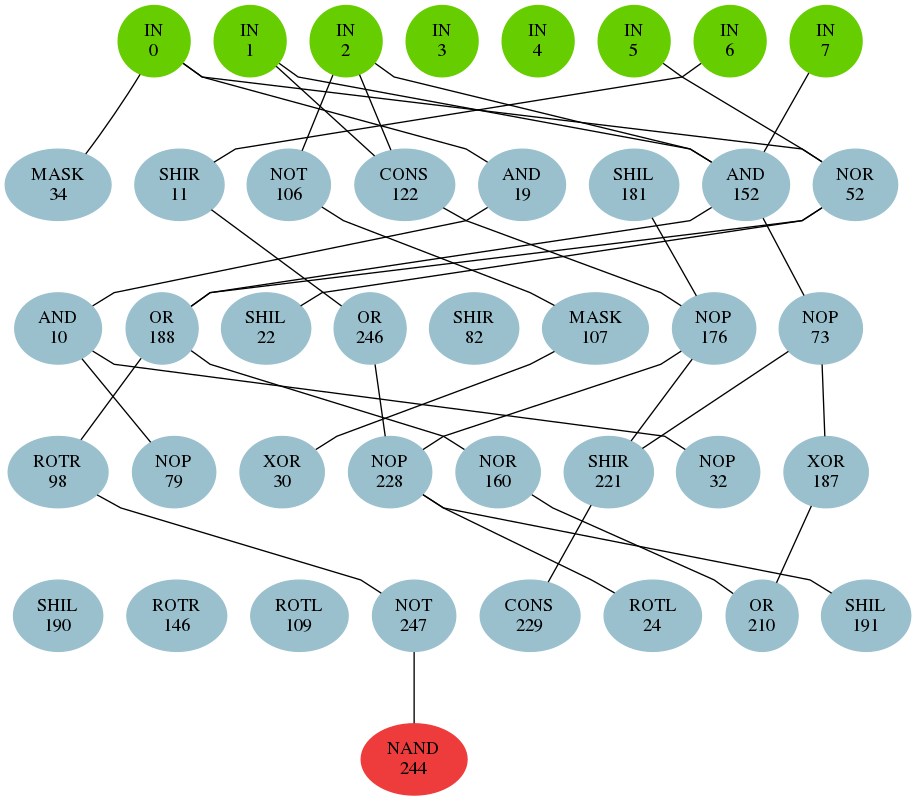
More important is the impact of the metaheuristics on cryptanalysis. The produced distinguisher is in form of simulated electronic circuit. This circuit can be analysed to find the source of non-randomness of the tested data. Formerly, the circuits were dense, hard to analyse. Guided local search metaheuristic forces the circuits to be sparser.

The left circuit was produced by former metaheuristic in EACirc (iterated local search), the right was produced by guided local search.

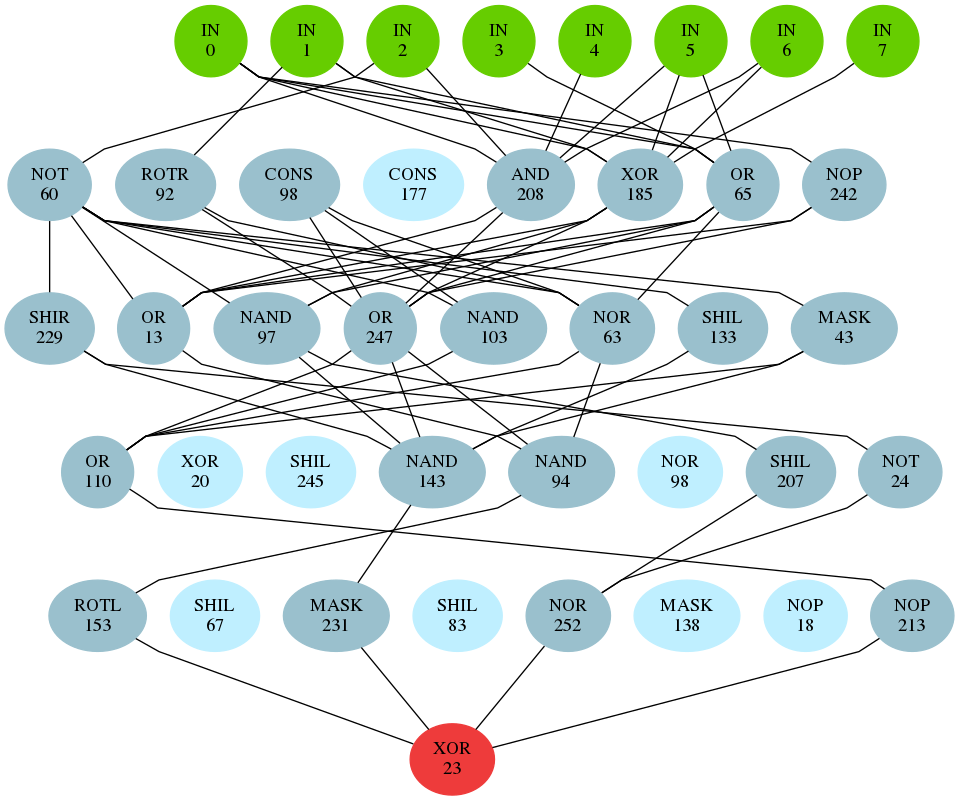
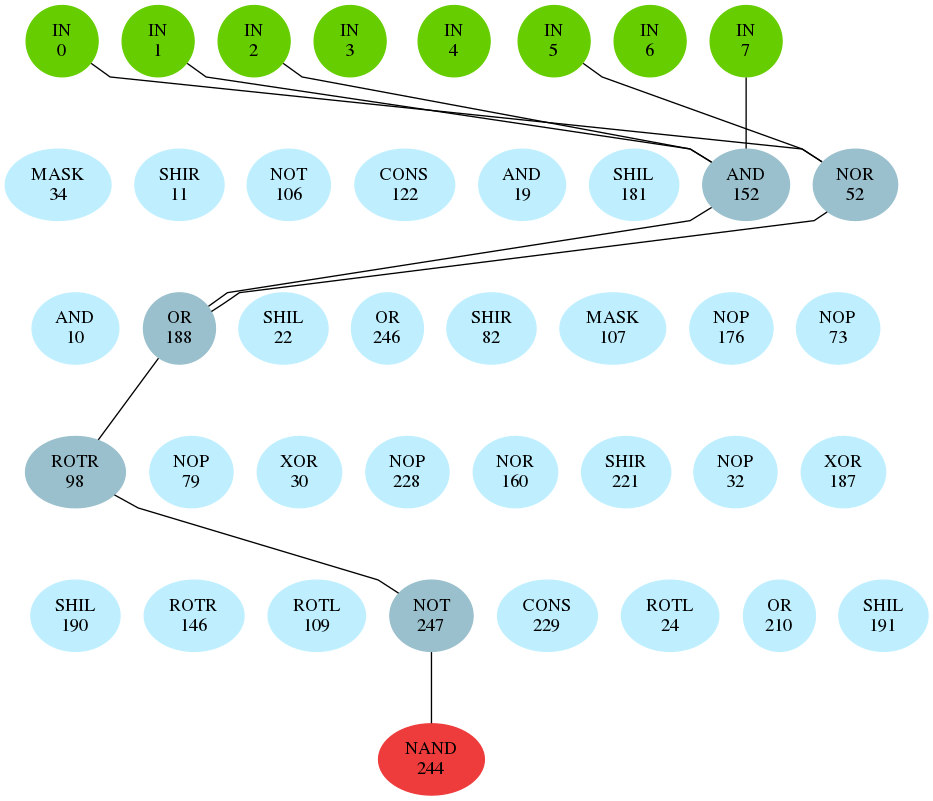
We can automatically remove unnecessary connectors from the circuits by pruning. This leads to the following circuits:

The left circuit is pruned circuit produced by former metaheuristic in EACirc (iterated local search), the right was produced by guided local search.

The pruned circuit from guided local search is much easier to analyse, which reduce the needed time for manual cryptanalysis of the cryptoprimitives.

Optimisation heuristics in randomness testing

Bibtex

Results