New results on reduced-round Tiny Encryption Algorithm using genetic programming

Authors: Karel Kubíček, Jiří Novotný, Petr Švenda, and Martin Ukrop

Abstract: Analysis of cryptoprimitives usually requires extensive work of a skilled cryptanalyst. Some automation is possible, e.g. by using randomness testing batteries such as Statistical Test Suite from NIST (NIST STS) or Dieharder. Such batteries compare the statistical properties of the function’s output stream to the theoretical values. A potential drawback is a limitation to predefined tested patterns. However, there is a new approach – EACirc is a genetically inspired randomness testing framework based on finding a dynamically constructed test. This test works as a probabilistic distinguisher separating cipher outputs from truly random data. In this work, we use EACirc to analyze the outputs of Tiny Encryption Algorithm (TEA). TEA was selected as a frequently used “benchmark” algorithm for cryptanalytic approaches based on genetic algorithms. In this paper, we provide results of EACirc applied to TEA ciphertext created from differently structured plaintext. We compare the methodology and results with previous approaches for limited-round TEA. A different construction of EACirc tests also allows us to determine which part of cipher’s output is relevant to the decision of a well-performing randomness distinguisher.

Bibtex: 

@article{eacirc-tea2016,
    title = {New results on reduced-round Tiny Encryption Algorithm using genetic programming},
    author = {Karel Kubíček and Jiří Novotný and Petr Švenda and Martin Ukrop},
    journal = {IEEE Infocommunications},
    volume = {8},
    number = {1},
    pages = {2--9},
    year = {2016},
    publisher = {Scientific Association for Infocommunications, Budapest, Hungary},
}

What is this paper about?

Automatized randomness testing is useful for checking one of the expected cipher properties – output ciphertext should be indistinguishable from a stream of truly random data. The common way to automate testing of randomness is using statistical batteries. But the limitation of the standard batteries for randomness testing is the fact they implement a fixed set of tests and can detect only a limited set of patterns and statistical irregularities.

In this work we use EACirc – a framework for constructing empirical tests of randomness. Capabilities of EACirc are compared with previous results as well as conventional statistical batteries analysing Tiny Encryption Algorithm.

EACirc consistently performs better than NIST STS. Dieharder is able to detect small deviances in one additional round. But analysis of EACirc output can provide information valuable for the cipher’s designer. We analyzed successful randomness tests and found the weak byte of limited TEA output.

In this we paper, we:

  • Give motivation for randomness testing and provided comparison of available tools.
  • Summarize approach of previous works based on evolution algorithms and extended it by our approach.
  • Analyze TEA limited to 1 to 5 rounds with different plaintext types using both statistical batteries and EACirc.
  • Interprete various results from statistical batteries and EACirc on different plaintext types.
  • Compare performance and data usage for many experiments settings.
  • Analyze resulting randomness test created by EACirc.

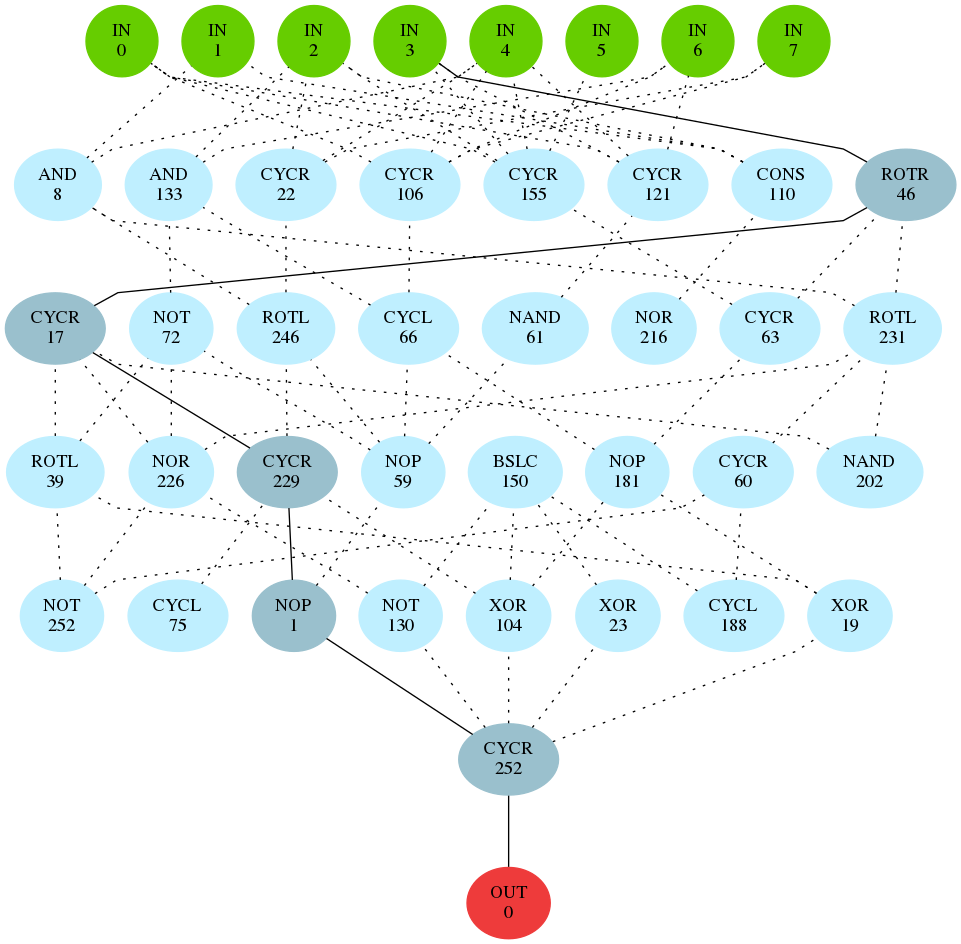
In the case of 4-round TEA on counter plaintexts (type 1), we analyzed several distinguishers with the fitness over 98%. In all of these circuits (see for example figure above) the distinguisher decision is based on the fourth byte of TEA ciphertext. The fourth byte is usually almost unchanged (operations affect only some bits).

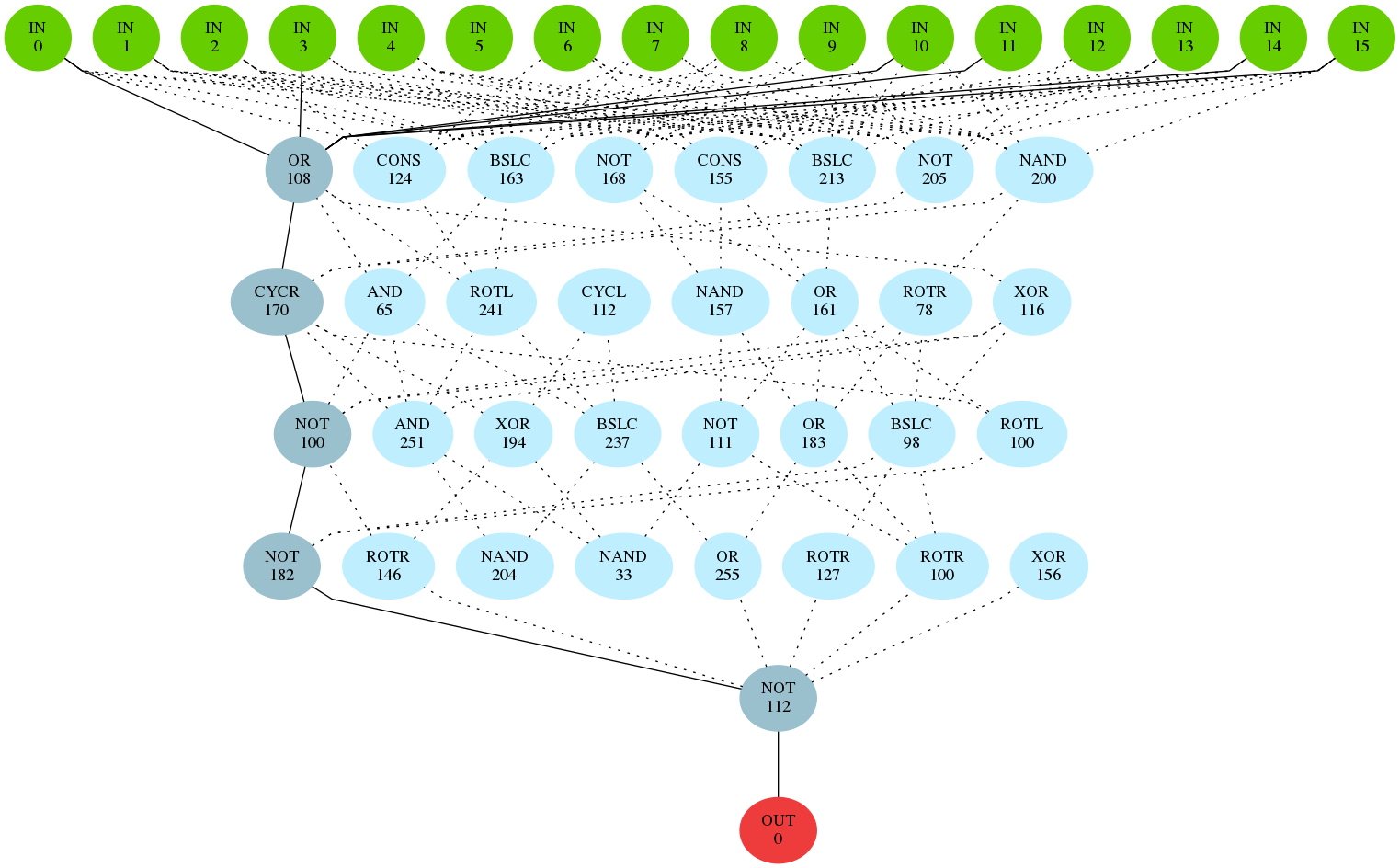
We also analyzed 4-round TEA on plaintexts suitable for strict avalanche criterion testing (type 3). In this case, the input layer had 16 input nodes, capable of processing two blocks of TEA ciphertext at once. Analyzed distinguishers (for example figure above) commonly combine the fourth byte of the first ciphertext block with the fourth byte of the second ciphertext block.